There are 2 main formulations of Special Relativity.
In Einstein’s original formulation, he postulated that the speed of light (c) remains the same in all inertial frames (and that the laws of physics remain the same in each inertial frame.)
He derived the Lorentz Transformations using what, to me, are rather tortuous arguments involving clocks, moving trains, bombs and so on. It’s also the way Feynman does it in “Six Not-So-Easy Pieces.”
You can see it done here and here if you like that kind of thing.
The Transformations, when they are finally produced, are usually written in the form :
Where is
(c being the speed of light, v the relative velocity of 2 observers).
After they’ve been derived in this way it really is necessary to learn them, because you sure as hell aren’t going to have time to derive them like this from first principles to order.
Fortunately, however, Minkowski came along after Einstein and made everything much clearer. He gave an alternative derivation of Special Relativity, which gives us a much more intuitive way to derive the equations from first principles.
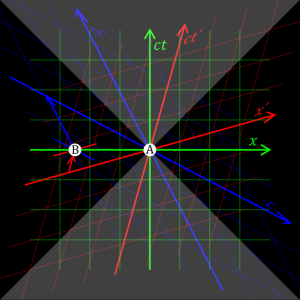
Minkowski postulated that spacetime is a 4-dimensional manifold with Minkowski inner product, signature (−,+,+,+).
This was his sole postulate.
The fact that c is constant in all inertial frames drops out as a direct consequence of the way the Minkowski inner product is defined. When a object travels at the speed of light in any reference frame, its interval is 0. The interval, you will recall, is a kind of “distance” on our manifold. The sign of the interval squared indicates whether 2 events can be casually related or not. Our object travelling at light speed is on the edge of the light cone illustrated below. If its interval is 0 in one frame, it’s 0 in all. Hence all observers have the same value for c. (So I suppose you could put it backwards and say that the Minkowski inner product takes the form it does so that c can remain constant in all reference frame.)
1. Recall the basic trig identity, .
2. Recall there is a hyperbolic equivalent. The only difference between the usual identity and the hyperbolic equivalent is a change of sign. .
3. As a consequence, in a desperate effort to find a transformation that might preserve the interval, write down a pleasing looking matrix.
This is the inverse of a Lorentz boost. It is simple to remember, much simpler than all the stuff with travelling clocks and bombs on trains. (It’s an inverse so we can write v instead of -v in our Transformations.) Lorentz boosts (and their inverses) preserve the spacetime interval.
4.. Now use this matrix to transform our original co-ordinates.
5. Multiply through. We get
6. Rewrite both equations as
and
7. Define .
This is the rapidity.
The equations in 6 above now read:
and
8. A little jiggling about gives
9. So substituting for in our 2 equations we have
as required.
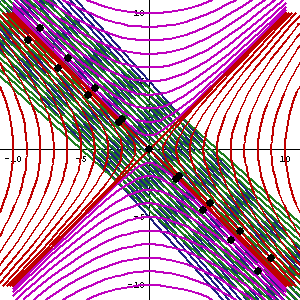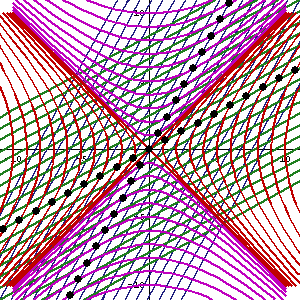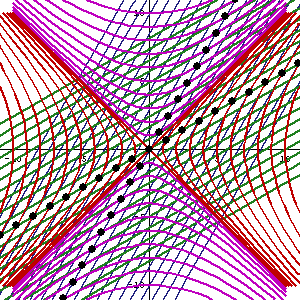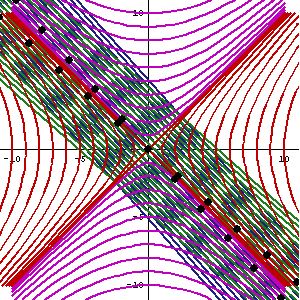
So what we have really done is view the Lorentz transformation as a hyperbolic rotation of coordinates in Minkowski space, (space-time) where the parameter represents the hyperbolic angle of rotation, often referred to as rapidity. (That bits from Wikipedia, as is the picture below of a hyperbolic rotation)
This hyperbolic rotation is what happens in space-time (or Minkowski) diagrams when the axes are squished together to introduce a new frame of reference.
The rotation is hyperbolic because of the minus sign in our Minkowski inner product, which leads us to the hyperbolic trig identity, which leads us to the matrix, which leads us to the Transformations.